Introduction
Pressure tests are vital in many industries, ensuring that systems handling gases and liquids are safe and dependable. They’re like health check-ups for pressurized equipment like pipelines, tanks, and other important equipment under pressure, making sure everything is working as it should from the safety point of view.
But, there’s a crucial factor that often gets overlooked: temperature. Just like how our body temperature can affect how we feel, temperature can also greatly impact how industrial equipment performs during Pressure tests.
Here, we’ll discuss how temperature influences pressure tests. We’ll start by laying down the basics, and understanding how gases and liquids behave under pressure. Then, we’ll dive into practical tips for controlling temperature during pressure tests, using real-world examples and strategies to help industry professionals navigate temperature’s influence effectively.
Understanding temperature’s impact is essential for ensuring precision, reliability, and safety in pressure testing practices across different industries.
So, let us start the journey and shed light on the critical relationship between temperature and pressure tests.
Understanding of the Governing Principles
Before delving into practical examples, laying down the theoretical groundwork that underpins the behaviour of gases and liquids under pressure is essential. Understanding these fundamental principles provides a solid foundation for how temperature influences pressure tests.
Air/Gas
Gases, by their very nature, exhibit behaviours that the ideal gas law can describe. when dealing with air or gases one must have the basic concept of the Ideal Gas Law.
Ideal Gas Law
The ideal gas law is a fundamental principle in thermodynamics that describes the behaviour of an ideal gas under various conditions. It relates the pressure, volume, temperature, and amount of gas present in a system and Mathematically, it is expressed by the equation:

Where:
- P is the pressure of the gas (in Pascals, Pa)
- V is the volume occupied by the gas (in cubic meters, m³)
- n is the number of moles of gas
- R is the ideal gas constant (J/(mol·K)) and
- T is the temperature of the gas measured in Kelvin.
According to the ideal gas law, Pressure and temperature are directly proportional, provided that the volume and the number of moles of gas remain constant. which means, an increase in temperature will lead to a proportional increase in pressure, and vice versa. This direct relationship between pressure and temperature is crucial to understanding the influence of temperature on gas pressure tests.
it concludes that as the temperature of a gas increases, its pressure will also increase, and conversely, a decrease in temperature will result in a reduction of pressure.
Mathematically, this relationship is expressed as:
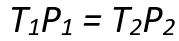
Where:
- P1 and P2 are the initial and final pressures (in Pascals, Pa), respectively,
- T1 and T2 are the initial and final temperatures measured in Kelvin, respectively.
Using the above equation, we can easily check the change in pressure concerning the temperature change.
Liquid
Liquids exhibit unique properties distinct from gases. While gases are highly compressible, liquids are generally considered to be incompressible. However, they demonstrate a degree of compressibility under pressure, though significantly less than gases.
While liquids are often deemed incompressible compared to gases, temperature changes can still impact their pressure levels. This influence stems from the relationship between temperature, pressure, and the bulk modulus, a fundamental property of liquids.
Bulk Modulus
The bulk modulus (B) is a fundamental property of liquids that quantifies their resistance to changes in volume under pressure.
The bulk modulus provides insights into how liquids respond to external pressure and is a critical parameter in understanding their behaviour under varying conditions
It represents the ratio of the change in pressure to the fractional change in volume. Mathematically, it is expressed as:
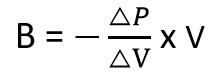
When the value of B is known, it is easy to calculate the effect of any pressure change on volume, or of any volume change on pressure using the equation below:

Where:
- B is the bulk modulus (in pascals, Pa)
- V is the initial volume of the liquid (in cubic meters, m³)
- ΔP is the change in pressure (in pascals, Pa) and
- ΔV is the volume change (in cubic meters, m³).
The bulk modulus provides insights into how liquids respond to external pressure and is a critical parameter in understanding their behaviour under varying conditions.
Coefficient of thermal expansion
Thermal expansion is the tendency of a fluid to expand due to an increase in temperature. The coefficient of thermal expansion can be used to relate temperature change to volume change, as shown in the following formula.
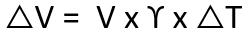
Where:
γ = Coefficient of cubical thermal expansion/°C at 100°C
∆T = Temperature rise, °C
The bulk modulus and the coefficient of cubical thermal expansion can be used together to compute the pressure change in a closed system subjected to a change in temperature.
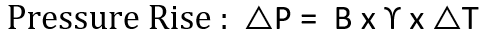
Looking into the above relation it can be concluded that as the temperature of a Liquid increases, its pressure will also increase, and conversely, a decrease in temperature will result in a reduction of pressure.
Some pressure test involves holding off the pressure for a longer duration and as discussed, the temperature always affects the pressure of the fluid taken for a pressure test.
The following strategies shall be adopted to have the correct monitoring of Pressure during test of any equipment :
- Controlled Testing Environments: Conduct pressure tests in environments where temperature variations can be minimized and controlled.
- Temperature Monitoring: Employ temperature monitoring devices to track and record temperature changes during the test continuously.
- Calibration Procedures: Calibrate pressure testing equipment to account for temperature variations and ensure accurate measurements.
- Correction Factors: Apply correction factors to compensate for temperature-induced changes in pressure and obtain precise results.